Abstract

This article proposes an approach to achieving faster transaction (pre)confirmations in Layer 2 blockchain networks through incremental block construction. We break down standard L2 blocks into smaller units, called \(\mathtt{Preconf Shreds}\), or \(\mathtt{Shreds}\), for faster processing and propagation. Preconfirmations are issued in batches via \(\mathtt{Shreds}\), enabling quick response to users while keeping the L2 blocks untouched.

The following outlines some key benefits of the proposed design.

• Reduced latency. By partitioning L2 blocks into smaller \(\mathtt{Shreds}\) and removing merkleization from the critical path, the system significantly reduces end-to-end transaction processing latency. The smaller block size enables faster processing and propagation through the network, while deferring resource-intensive merkleization until the full L2 block is complete.
• Fast preconfirmations. Users receive preconfirmations almost immediately because each \(\mathtt{Shred}\) is processed quickly, without waiting for the entire L2 block to be completed. Since \(\mathtt{Shreds}\) are smaller and do not require merkleization, users can receive confirmations multiple times faster than traditional approaches.
• Early state updates. With \(\mathtt{Shreds}\), network nodes can update their local state as soon as a \(\mathtt{Shred}\) arrives, rather than waiting for the full block. This enables faster state synchronization across the network and allows applications to work with the most current state data.
• Efficient merkleization. The design improves merkleization efficiency by deferring merkleization until the full L2 block is complete. Changes are batched together for more efficient processing. Additionally, the system can prefetch required trie nodes during \(\mathtt{Shred}\) execution, reducing disk I/O overhead during final merkleization. The combination of batched updates and prefetching significantly reduces the computational cost of merkleization compared to traditional approaches.

Acknowledgements

Inspiration for this work came from Solana Shreds, Kubi Mensah's work on Based Sequencing, and many discussions with the Fabric teams.

Background

In blockchain networks, particularly L2s, transaction confirmation speed and state synchronization are critical challenges that impact network performance and user experience. Traditional approaches to block building and state management often introduce latency and inefficiencies that limit the potential for scalability. This section explores the fundamental concepts and challenges in current blockchain architectures, focusing on block building processes, merkleization overhead, and state propagation mechanisms.

Block Building & Merkleization

Merkleization

Merkleization is the process of creating a Merkle-Patricia Trie (MPT) - a data structure that efficiently summarizes and verifies global state data. Merkleization generates a succinct \(\mathtt{stateRoot}\) serving as the commitment to the global state and helps safe-guard against any invalid state.

When updating a key, the MPT need to update all nodes along the path from the root node to the targeted leaf node to ensures state consistency. As the state grows, the number of internal nodes required to be updated also increases.

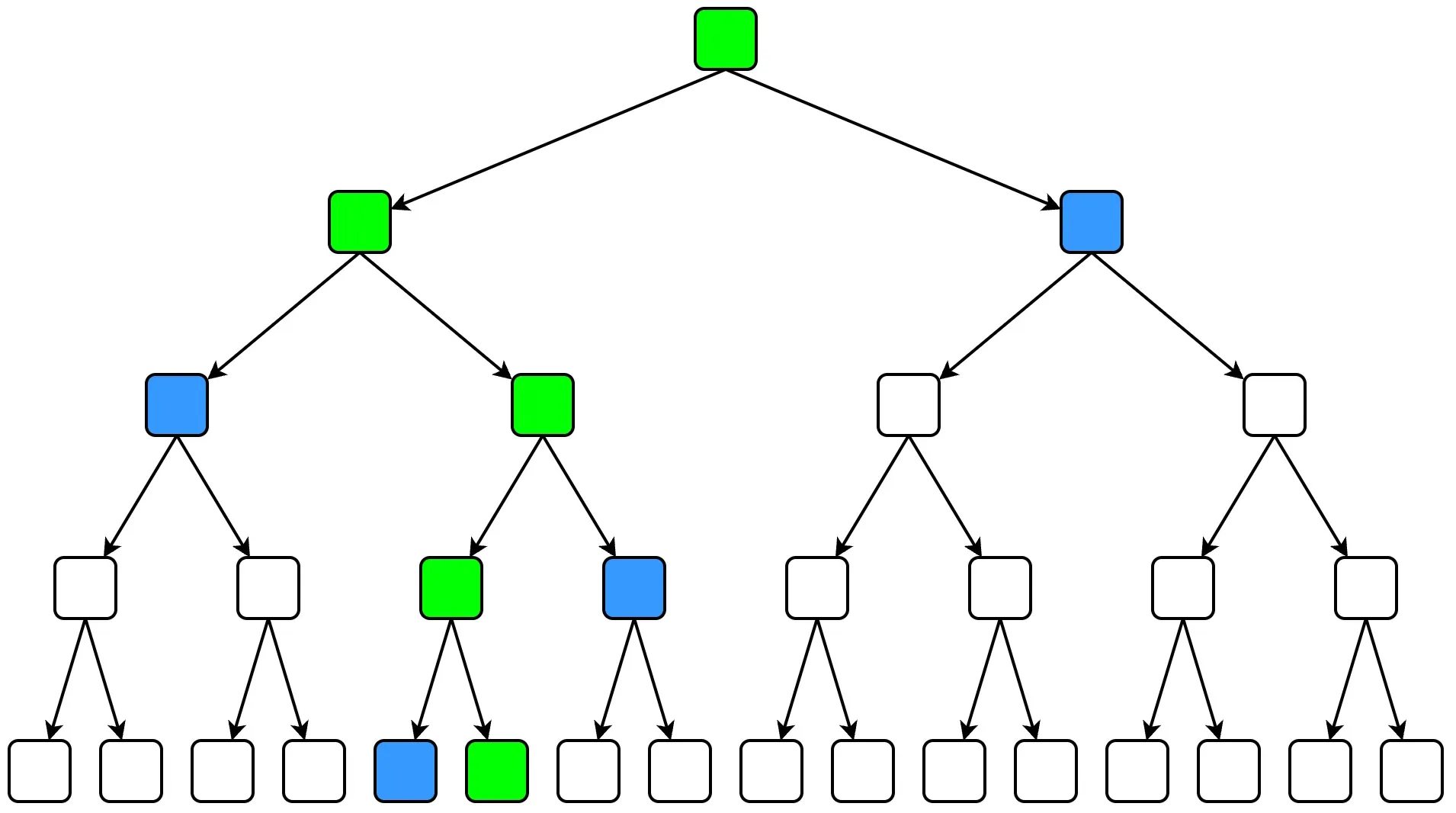
In the current block building pipeline, merkleization must be done on the critical path. In other words, to commit a block, a new \(\mathtt{stateRoot}\) must be available.

Execution and Merkleization Separation

To address merkleization performance issues, many Ethereum clients separate their databases for execution and merkleization. During execution, block executors use a flat database (flatDB) to read states. The flatDB provides \(\mathcal{O}(1)\) time complexity for reading and writing key-value pairs-much faster than the MPT's log-squared complexity, enabling fast block executions. All changes to keys are recorded in a \(\mathtt{ChangeSet}\). After block execution completes, the merkleization process updates the MPT with all changes from the \(\mathtt{ChangeSet}\) to generate the full state commitment.

Despite this database separation, merkleization still depends on execution results, which makes parallel processing impossible. Worse yet, merkleization consumes a significant portion of the end-to-end block production process. In Ethereum, merkleization takes up to 75% of the E2E time to seal a block, and this percentage can exceed 90-95% with shorter blocktime.

Batch Updates to MPTs

It is worth noting that batch updates to an MPT are always more efficient than separate updates under the same workload. This is easy to understand as nodes on higher levels are most likely to be touched multiple times because keys might share the same prefix.

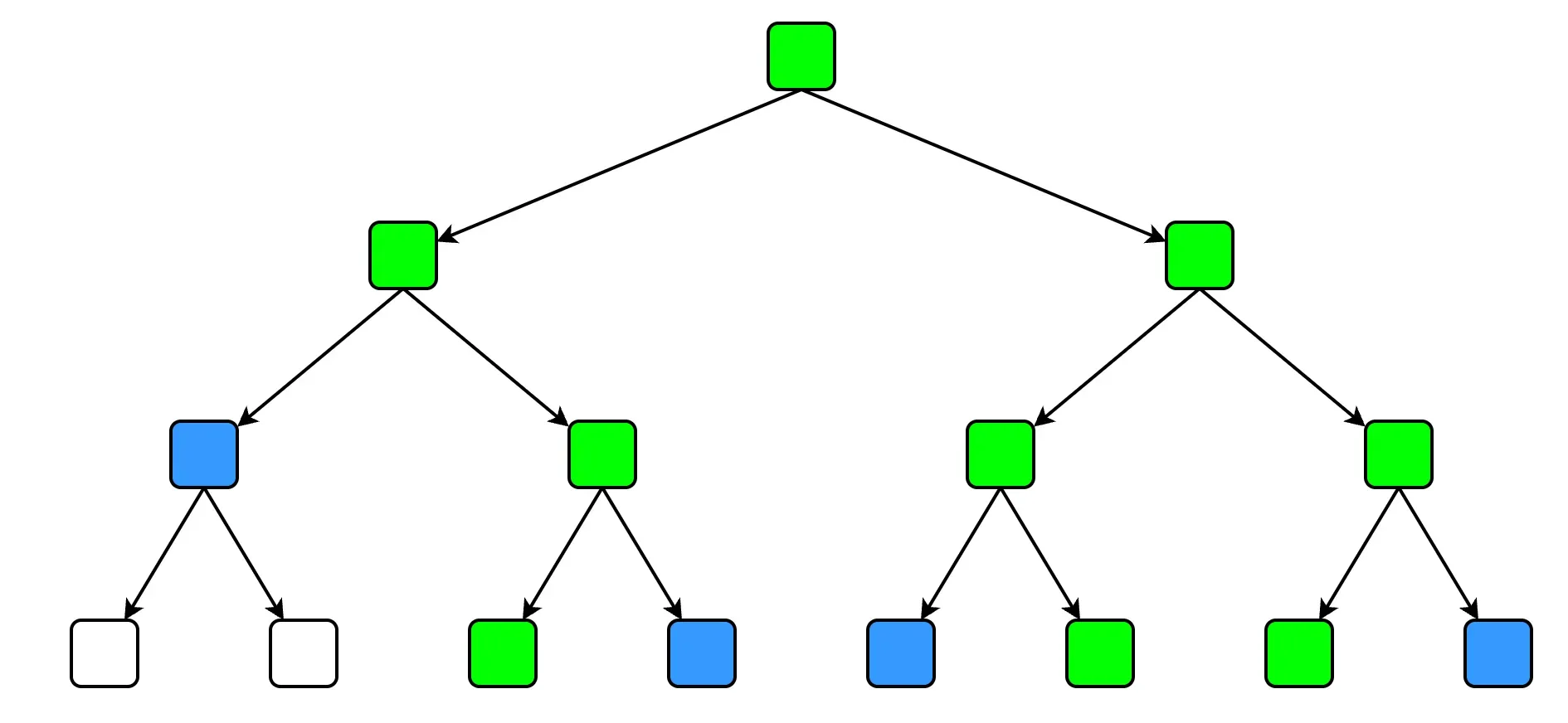
Merkleization and Blocktime Reduction

Transaction confirmation speed is crucial for user experience and network efficiency. Users need fast transaction confirmations, particularly for time-sensitive applications like payments and decentralized exchanges. Slow confirmations frustrate users and limit blockchain adoption.

While most rollups achieve quick confirmations through shorter blocktime, the requirement for merkleization in the critical path makes it challenging to achieve sub-second blocktime. Therefore, in order to reduce blocktime, the most prioritized task is to reduce the affect of merkleization to block producing.

Block Propagation

State synchronization ensures that all participating nodes in a network maintain a consistent view of the shared state, which is essential for the integrity and reliability of the system. In a rollup, this process typically involves the propagation of new blocks from a sequencer node to follower nodes. The conventional method involves the sequencer propagating a block only after it is fully constructed.

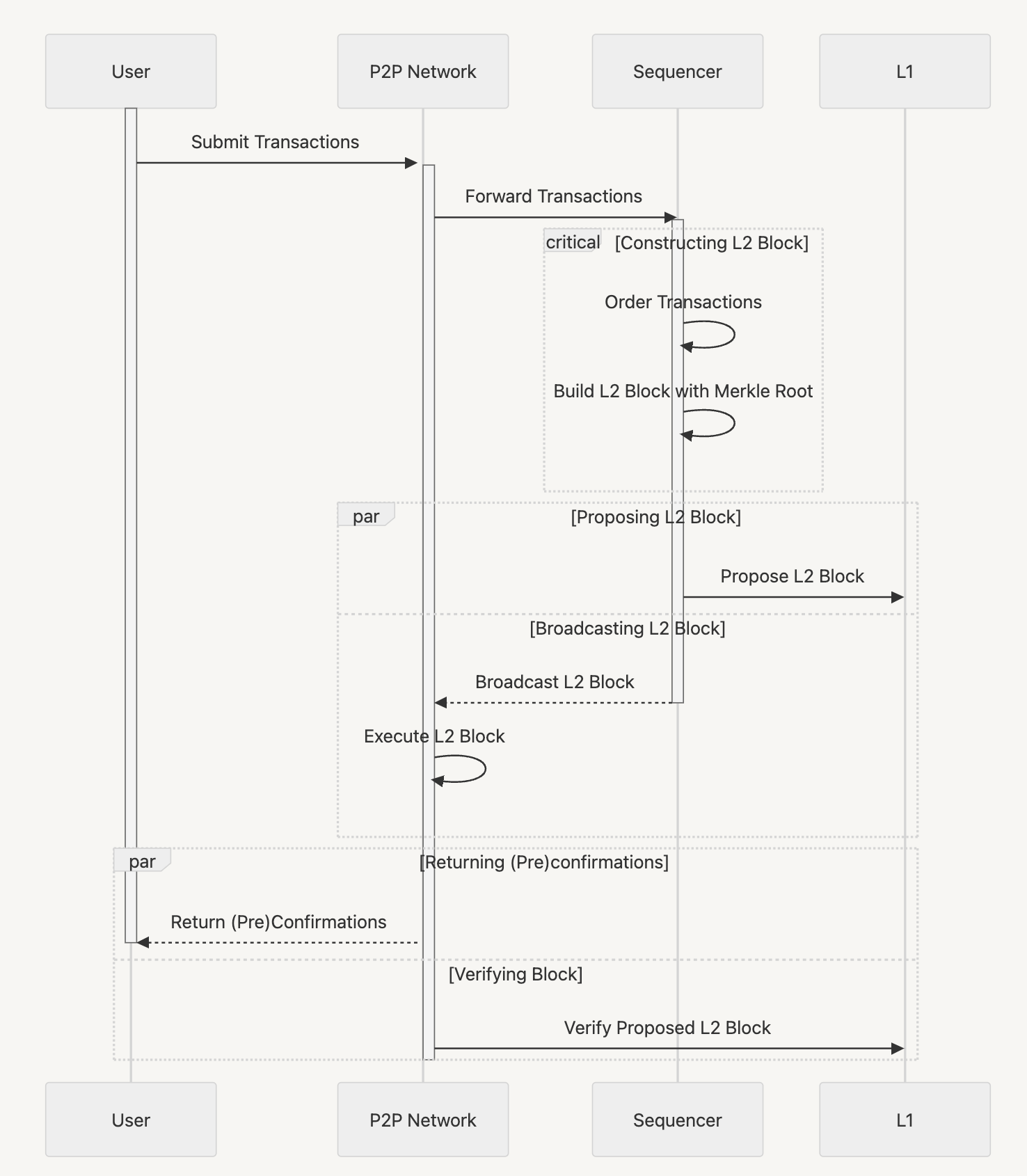
However, this approach can introduce latency and hinder overall system performance, especially with larger block sizes as propagating the entire block at once introduces latency. This latency becomes more pronounced with larger block sizes and limited network bandwidth. Larger blocks, while accommodating more transactions, can also lead to increased block propagation time, further amplifying latency.

Fast Preconfirmations via Incremental Block Construction

In this section, we introduce a solution that leverages incremental block construction to achieve faster transaction confirmations while maintaining the security guarantees of traditional block building. Our solution addresses the key challenges of merkleization overhead and block propagation latency by introducing \(\mathtt{Shreds}\) - smaller, separately verifiable units that enable rapid preconfirmations without compromising the integrity of the system.

The core innovation lies in partitioning canonical L2 blocks into smaller segments that can be processed, verified, and propagated separately. This approach allows us to remove merkleization from the critical path of transaction confirmation while ensuring that the final block maintains all necessary security properties.

Terminology

• L2 (Canonical) Block. A block generated every L1 block period (12 seconds) that contains a set of ordered transactions and their state changes.
  • Each L2 block includes a \(\mathtt{stateRoot}\) that represents the global state commitment after applying all transactions within the block.
  • L2 blocks are partitioned into smaller \(\mathtt{Shreds}\) for faster propagation and preconfirmations.
• \(\mathtt{Shred}\). A segment of a canonical L2 block that contains a subset of transactions and their state changes.
  • A \(\mathtt{Shred}\) does not perform merkelization but records the \(\mathtt{ChangeSet}\) commitment to all state modifications instead.
  • A \(\mathtt{Shred}\) is somewhat similar to a \(\mathtt{Frag}\) introduced in a recent article from Gattaca.
• \(\mathtt{ChangeSet}\). A key-value mapping that records all state modifications within a \(\mathtt{Shred}\).
  • A \(\mathtt{ChangeSet}\) must also expose an efficient method to calculate the commitment to its data.

Incremental Block Construction

\(\mathtt{Shreds}\)

At a high level, we assume a canonical L2 block has the same blocktime as the L1 (i.e, 12 seconds). There is exactly one L2 block corresponding to an L1 block. Similar to Solana’s shreds and Unichain’s Flashblocks, an L2 block is split into multiple sub-blocks called \(\mathtt{Shreds}\).

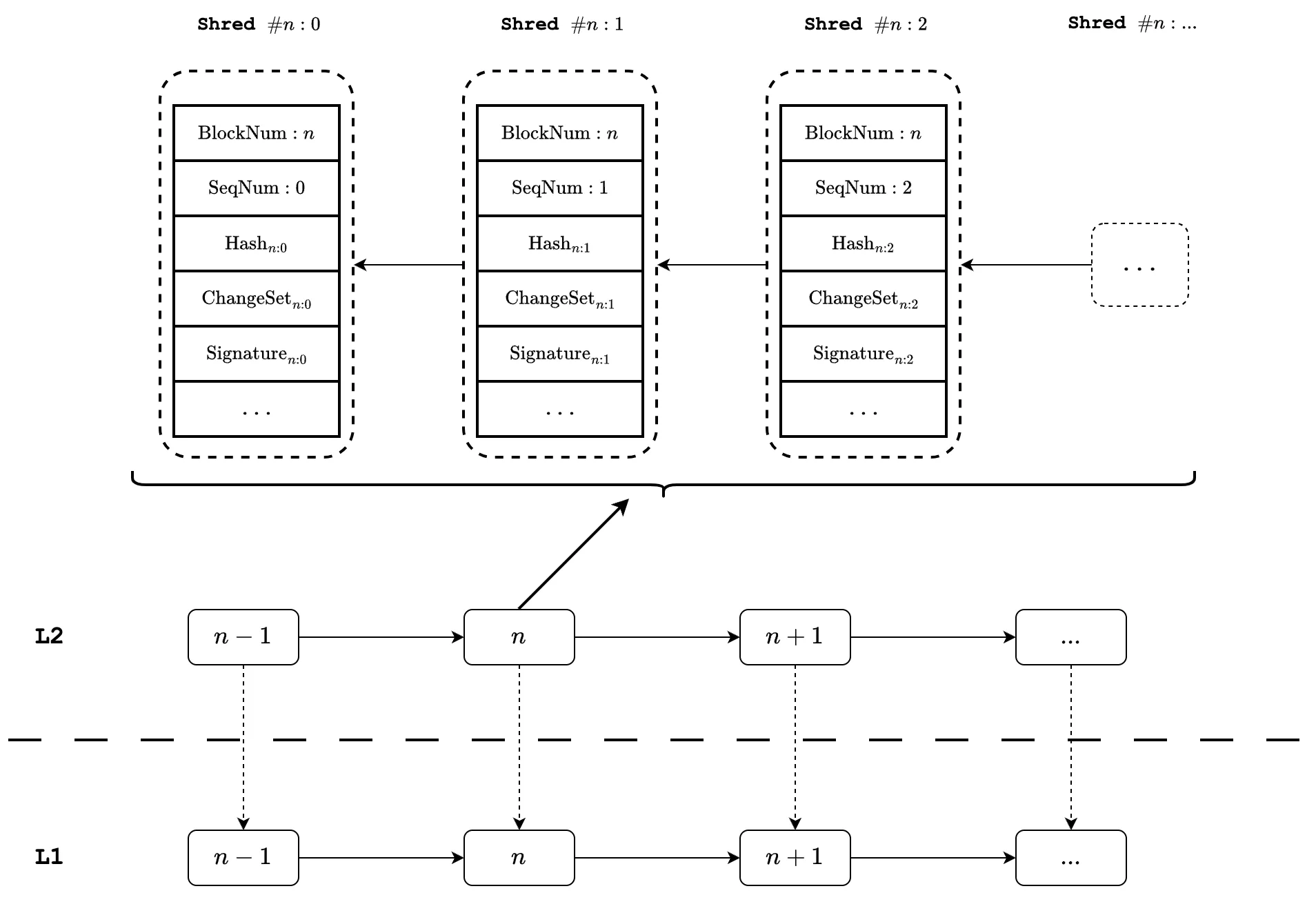
\(\mathtt{Shreds}\) partition an L2 block into multiple consecutive, connecting segments. Each \(\mathtt{Shred}\) for an L2 block is identified via its sequencer number. In other words, block_num and seq_num together can always identify a \(\mathtt{Shred}\). The sequence number is increasing for each \(\mathtt{Shred}\) and is reset when a new L2 block is constructed.

A \(\mathtt{Shred}\) contains a changeset_root that commits to all state changes made within the \(\mathtt{Shred}\). Recall that during execution, the sequencer uses the flatDB to access data and records all changes to a \(\mathtt{ChangeSet}\). The number of entries in a \(\mathtt{ChangeSet}\) is relatively small compared to the state size because it only holds the changes, therefore, the data is often sparse and can fit in memory. As a result, constructing the changeset_root can be efficiently done.

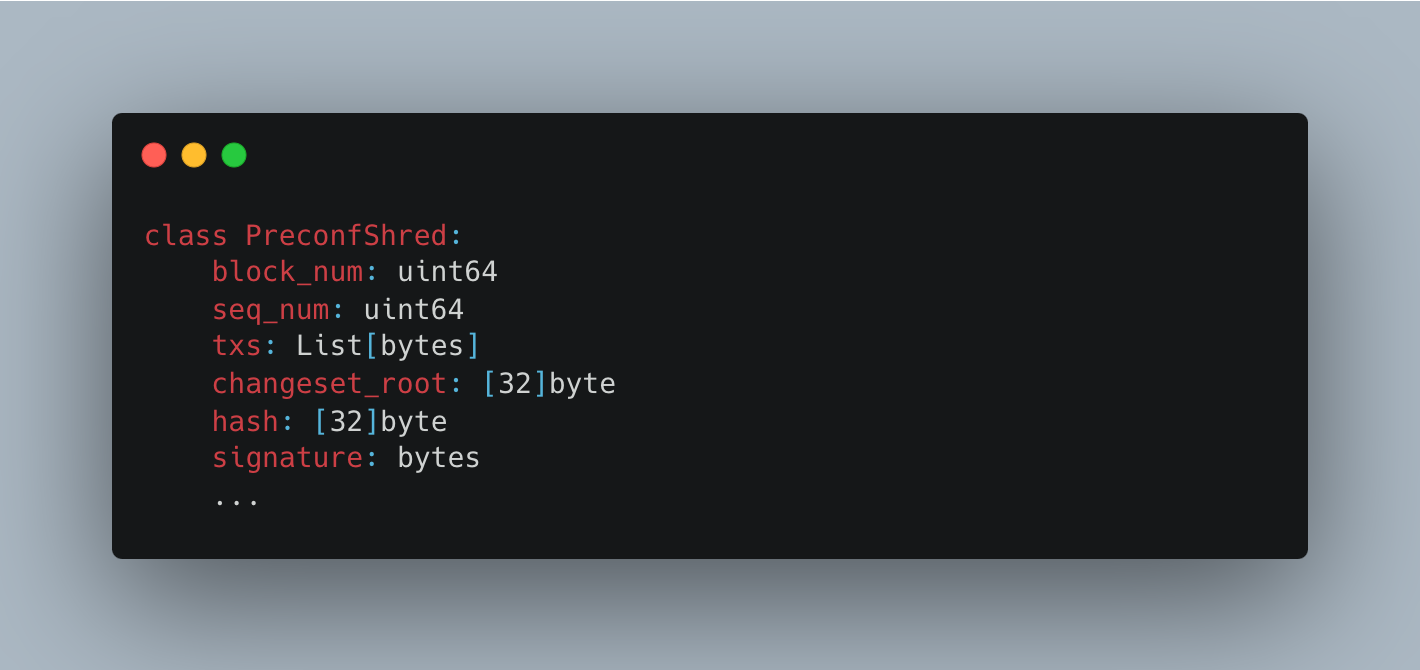
Finally, each \(\mathtt{Shred}\) contains a sequencer signature on all of its content. The signature is required for slashing upon misbehaviors. Examples of misbehaviors include:

• Signing two \(\mathtt{Shreds}\) with the same block_num and seq_num.
• Signing non-consecutive \(\mathtt{Shreds}\) (\(\mathtt{Shreds}\) with non-consecutive seq_num's) for a given L2 block.
• changeset_root does not match the actual changeset_root after applying transactions.
• etc,.

Note that the \(\mathtt{Shred}\) blocktime can be configured to balance multiple factors, including preconfirmation latency and network bandwidth.

Annotated Workflow

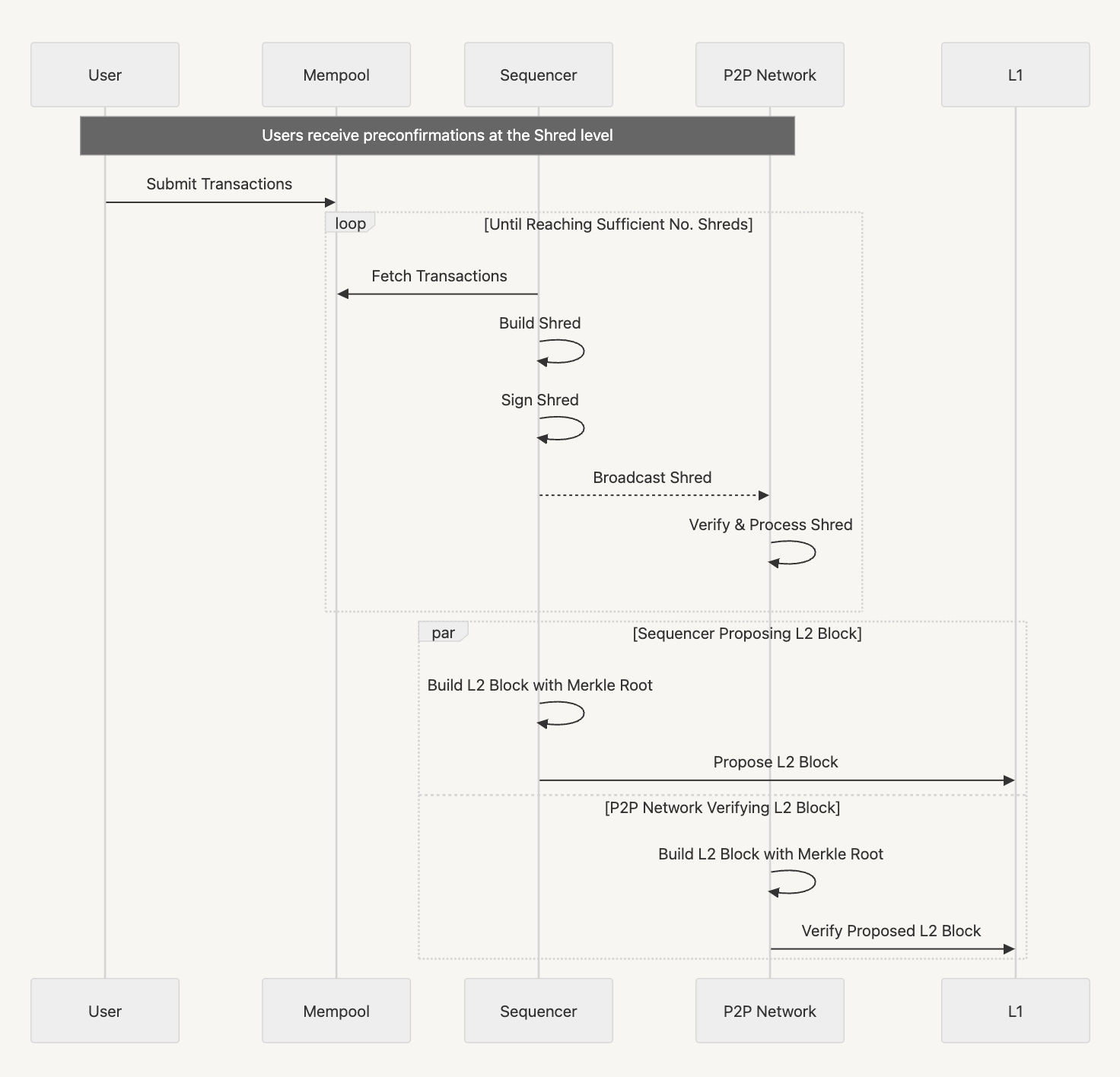
• Transactions in mempool are incrementally batched into \(\mathtt{Shreds}\) following pre-defined ordering rules. A \(\mathtt{Shred}\) only commits to changes within its transactions and does not perform merkleization. This enables fast \(\mathtt{Shred}\) with higher throughput than regular blocks.
• Once a \(\mathtt{Shred}\) is built, it is immediately broadcasted to all following nodes in the P2P network. This \(\mathtt{Shred}\) serves as preconfirmations for all transactions it contains, providing users with blocktime multiple time faster than usual.
• When a node receives a \(\mathtt{Shred}\), it immediately verifies and processes all included transactions. The sequencer's signature on each \(\mathtt{Shred}\) enables enforcement through slashing if misconduct occurs.
• Once the number of \(\mathtt{Shreds}\) reach a threshold (e.g, if \(\mathtt{Shred}\) blocktime is 100ms, an L2 block consists exactly 120 \(\mathtt{Shreds}\)), an L2 block is finalized by adding required information such as \(\mathtt{stateRoot}\). This is when merkleization happens. Note that the canonical L2 block has been incrementally built right from the first \(\mathtt{Shred}\).
• The canonical L2 block is then proposed to L1.

Block Propagation

Broadcasting is done per \(\mathtt{Shred}\) instead of waiting for the full L2 block. \(\mathtt{Shreds}\) with invalid signatures are discarded. As peer nodes receive valid \(\mathtt{Shreds}\), they optimistically construct a local block and provide preconfirmations to users.

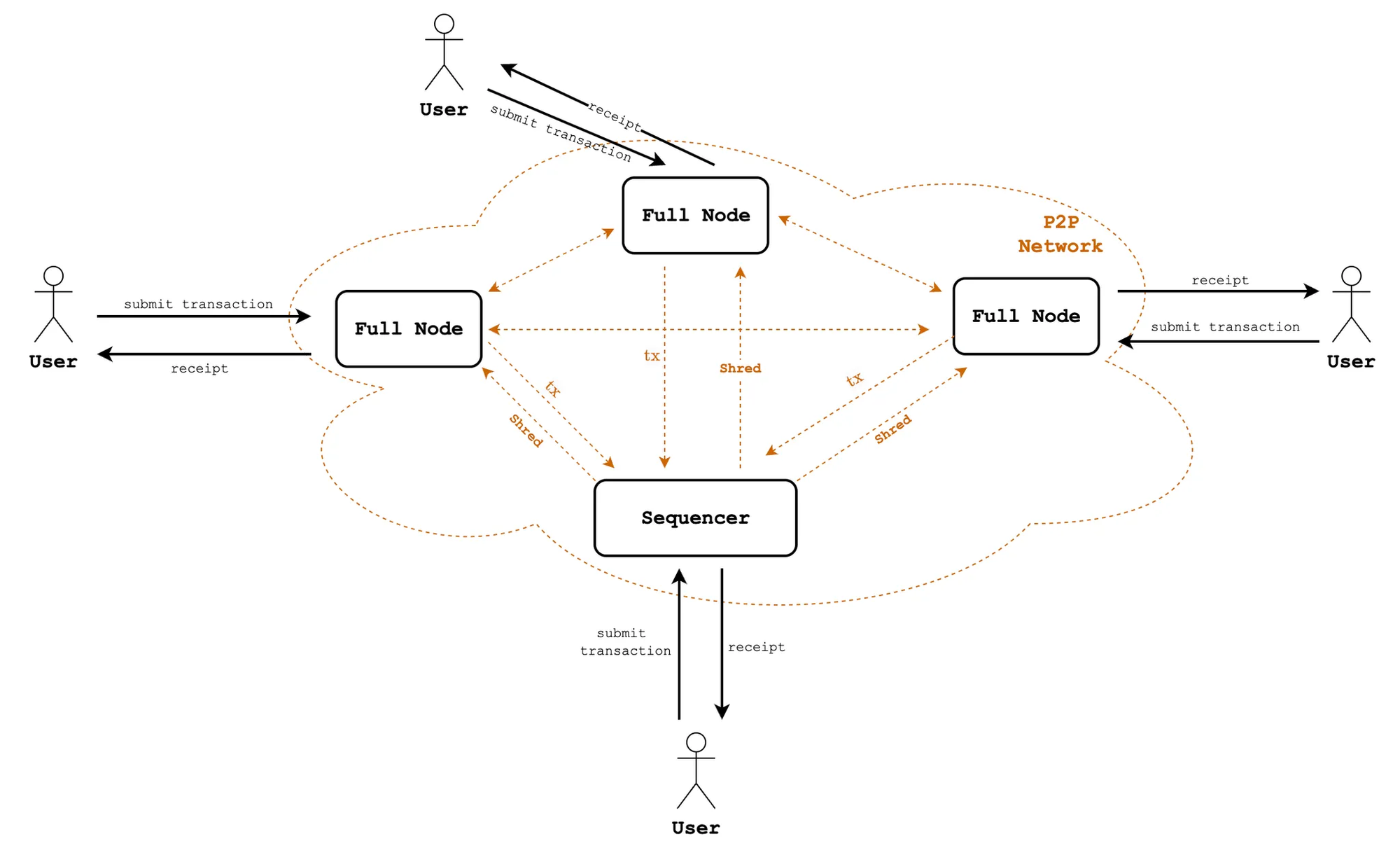
The sequencer might also broadcast the \(\mathtt{ChangeSet}\) within a \(\mathtt{Shred}\)to its peers. This \(\mathtt{ChangeSet}\) can be verified against the changeset_root attached to the \(\mathtt{Shred}\)’s header. Nodes trusting the sequencer can apply the \(\mathtt{ChangeSet}\) immediately to their local state without re-executing transactions.

Efficient Merkleization

As mentioned above, merkleization's performance is influenced by both the size of state data and the number of changes (i.e., the size of the \(\mathtt{ChangeSet}\)). Additionally, batch updates are more efficient than sequential updates.

Merkleization for an L2 block only happens after the last \(\mathtt{Shred}\) is generated. Accumulating changes over multiple \(\mathtt{Shreds}\) reduces the number of final keys that need updating, thanks to transaction overlap. The same data is likely to be accessed multiple times across blocks, especially with popular dApps like Uniswap.

Prefetching can also be used to efficiently load MPT’s trie nodes into memory prior to the actual merkleization. The idea behind this technique is that, during execution of \(\mathtt{Shred}\) \(i\), we can prefetch all keys in the \(\mathtt{ChangeSets}\) of \(\mathtt{Shreds}\) \(i-1\) and before.

Further Considerations

While incremental block construction offers a promising path to lower blockchain latency, realizing its full potential hinges on addressing several key challenges. In this section, we outline the open questions and future research directions.

• \(\mathtt{Shred}\) Slashing. Sequencers who misbehave when creating \(\mathtt{Shreds}\) will be penalized (slashed). The specifics of slashing mechanisms are beyond this article's scope.
• Fraud Proofs. Fraud proofs can still be performed between L2 blocks in the traditional manner, though this requires careful considerations.
• State Proofs for \(\mathtt{Shreds}\). Accumulated \(\mathtt{ChangeSets}\) and the previous \(\mathtt{stateRoot}\) (of the most recent L2 block) can be used to prove state data inclusion/exclusion at any \(\mathtt{Shreds}\).
• \(\mathtt{ChangeSet}\) Design. \(\mathtt{ChangeSets}\) must support basic CRUD operations and inclusion/exclusion proof generation. However, several key design questions remain.
  • What is the optimal data structure for instantiating a \(\mathtt{ChangeSet}\)?
  • Should \(\mathtt{ChangeSets}\) accumulate changes over time?
  • And so on.

Addressing these concerns is crucial for realizing the full potential of increment block construction. While this article introduces the framework, this is an ongoing research project. We will elaborate on the technical details, including algorithm specifications, data structures, and present formal results and implementation specifics in subsequent articles.